하지만 교과서 공부, 논문 읽기, 소스 코드 읽기 및 쓰기, 블로그 작성 등 기계 학습에 대해 깊이 파고 들면서 내가 한 일들을 묘사하는데 사용되는 몇몇 용어들이 생각보다 이해하기 어렵다는 것을 알게 되었습니다. 예를 들자면 categorical cross-entropy loss가 무엇인지, 어떤 일을 하며 어떤 식으로 정의되는지는 이해했지만 도대체
"왜 이런 녀석들을 negative log-likelihood라 부르는 것인가?"와 같은 의문들이 생기기 시작했습니다.
시간이 지나 이제는 위 질문에 대해 적어도 두 가지 정도는 알게 되었습니다:
- 우리가 "기계 학습"이라 부르는 기술들(classification and regression models)은 거의 대부분 통계를 기반으로 하고 있다. 때문에 용어들이 두 분야에서 혼용되고 있다.
- 대부분의 용어가 새로 만들어진 것이 아니다.
이 글에서는 제가 깨달은 사실을 바탕으로 우리가 잘 알고 있고, 자주 사용하며, 어떻게 사용하는지 알고 있는 세가지 모델들이 수학적으로 어떤 역할을 하는 것인지 설명하고자 합니다. 기본적으로 독자들이 기계학습과 통계학 분야의 개념들에 대해 익숙하다는 가정 하에 글을 쓸 것이며 두 분야 사이의 연관성에 대해 더욱 깊은 이해를 위해 서서히 파고들 생각입니다. 수학이 들어가긴 하지만 딱 필요한만큼만 사용할 것이고 유도의 대부분은 결과없이 건너 뛸 수도 있습니다.
어떤 predictive model을 제품화할 때는,
import sklearn으로 다른 사람이 만들어 둔 모델을 사용하는 것이 최고의 방법이자 보통 우리가 알고 있는 방식입니다. 그렇기에 이 글은 여기서 시작해서 결국에는 다시 이 지점으로 돌아올 것입니다. 다만 이전과 다른 점은 그 밑바닥을 잘 알고 사용할 수 있겠습니다. (글쓴이는 이 과정을 마치 수영장에서 다이빙 하고, 밑바닥을 찍고, 다시 표면으로 올라오는 모습과 비슷하게 생각했는지 같은 은유를 수차례 사용합니다.) Lemma들은 굵은 글씨체로 작성되어 있습니다.
먼저 우리가 앞으로 다룰 세 개의 주요 모델들을 만나보시겠습니다. 편의를 위해 코드는 Keras로 통일합니다.
Linear regression with mean squared error
input = Input(shape=(10,))
output = Dense(1)(input)
model = Model(input, output)
model.compile(optimizer=_, loss='mean_squared_error')
Logistic regression with binary cross-entropy loss
input = Input(shape=(10,))
output = Dense(1, activation='sigmoid')(input)
model = Model(input, output)
model.compile(optimizer=_, loss='binary_crossentropy')
Softmax regression with categorical cross-entropy loss
input = Input(shape=(10,))
output = Dense(3, activation='softmax')(input)
model = Model(input, output)
model.compile(optimizer=_, loss='categorical_crossentropy')
다음으로 response variable, functional form, loss function, loss function + regularization term 이렇게 네 가지 주요 요소들이 있는데요 앞으로 세 가지 모델들에 대해 각 요소가 어떤 통계적인 의미를 지니는지 알아보도록 하겠습니다 (수영장 밑바닥에서 한 계단씩 올라가겠습니다).
잠깐! 완전히 잠수하기 전에 준비운동부터 해야겠죠? 몇 가지 중요한 개념들에 대해 정의하고 넘어가겠습니다.
Random variable
저(글쓴이)는 random variable을 "여러가지 다른 값들을 가질 수 있는 것"이라고 정의합니다.
- "The tenure of despotic rulers in Central Africa" is a random variable. It could take on values of 25.73 years, 14.12 years, 8.99 years, ad infinitum; it could not take on values of 1.12 million years, nor -5 years.
- "The height of the next person to leave the supermarket" is a random variable.
- "The color of shirt I wear on Mondays" is a random variable. (Incidentally, this one only has ~3 distinct values.)
Probability distribution
확률 분포란 random variable이 갖는 값을 관측할 likelihood에 대한 일종의 lookup table이라 할 수 있습니다. 주어진 variable이 {비, 분, 진눈깨비, 우박} 중 하나의 값을 가진다고 할 때, 다음과 같이 probability distribution으로 나타낼 수 있습니다:
p = {'rain': .14, 'snow': .37, 'sleet': .03, 'hail': .46}
당연하지만, 모든 값의 합은 1이어야 하지요.
- 확률 질량 함수는 이산 값을 갖는 random variable 확률 분포다.
- 확률 밀도 함수는 연속 값을 갖는 random variable의 확률 분포를 주는 함수다.
- 여기서 "주는"이라고 표현한 까닭은 이 함수 스스로는 lookup table이 아니기 때문이다. 즉 값이 [0,1] 범주 안에서 주어진 random variable에 대해 $Pr(X=0.01), Pr(X=0.001),Pr(X=0.0001),~etc.$를 정의할 수 없다.
- 대신 일정 범위 안에서 어떤 값을 관측할 확률을 알려줄 수 있는 함수를 하나 정의하여 사용할 수 있다: e.g. $Pr(0.01<X<0.4)$
- 이 것이 확률 밀도 함수이며 $Pr(0\leq X \leq 1)=1$을 만족한다.
Entropy
엔트로피는 주어진 결과에 도달할 수 있는 방법의 가짓수를 정량화 해줍니다. 8명의 친구들이 두 대의 택시를 나눠타고 브로드웨이 쇼를 보러 가는 것을 상상해보죠. 다음과 같이 두 가지의 시나리오를 생각해보겠습니다:
# fill the first, then the second
assignment_1 = [1, 1, 1, 1, 2, 2, 2, 2]
# alternate assignments
assignment_2 = [1, 2, 1, 2, 1, 2, 1, 2]
# alternate assignments in batches of two
assignment_3 = [1, 1, 2, 2, 1, 1, 2, 2]
# etc.
- 모든 친구들이 하나의 택시에 어떻게든 우겨 탄다:
assignment_1 = [1, 1, 1, 1, 1, 1, 1, 1]
두 번째 경우보다 첫 번째 경우가 가능한 경우의 수가 많기 때문에 첫 번째 결과(outcome)가 더 높은 엔트로피 값을 갖게 됩니다.
More explicitly,
엔트로피를 확률 분포에 대해 계산을 해보면 다음과 같습니다:
$$H(p)=-\sum_{i=1}^n p_i \log p_i$$
이 때,
- 총 서로 다른 n개의 이벤트가 존재한다.
- 각 이벤트 $i$는 $p_i$의 확률을 갖는다.
엔트로피는 가능한 이벤트들에 대한
weighted-average log probability이고, (이는 수식에서 더 명백히 알 수 있는데) 분포에 내재한 불확실성을 측정하는 방법이라 할 수 있습니다. 즉, 어떤 이벤트에 대해 엔트로피가 높다는 것은 해당 결과값을 얻을 것이라는 믿음에 대한 확실성이 덜하다는 것을 뜻하죠.
위에서 언급한 확률 분포에 대해 엔트로피를 계산해보겠습니다.
p = {'rain': .14, 'snow': .37, 'sleet': .03, 'hail': .46}
def entropy(prob_dist):
return -sum([ p*log(p) for p in prob_dist.values() ])
In [1]: entropy(p)
Out[1]: 1.1055291211185652
비교를 위해 두 개의 분포를 더 만들어서 각각의 엔트로피들을 계산해보겠습니다.
p_2 = {'rain': .01, 'snow': .37, 'sleet': .03, 'hail': .59}
p_3 = {'rain': .01, 'snow': .01, 'sleet': .03, 'hail': .95}
In [2]: entropy(p_2)
Out[2]: 0.8304250977453105
In [3]: entropy(p_3)
Out[3]: 0.2460287703075343
첫 번째 분포에서 우리는 내일 날씨가 어떨 지에 대해 가장 확신이 없습니다. 이에 맞게 엔트로피도 가장 높습니다. 세 번째 분포의 경우 내일의 날씨가 우박일 것이라는 것에 가장 확신을 가질 수 있을 것이고 엔트로피도 역시 작은 것을 볼 수 있습니다.
마지막으로 택시 예화에서도 마찬가지로 오직 한 가지 경우만 가능한 분포에 비해 여러 갈래로 이벤트가 생길 수 있는 분포에 대해 엔트로피 값이 낮다는 것을 알 수 있습니다.
이제 준비운동을 마쳤으니 수영장에 들어가야겠지요. 그럼 가장 바닥부터 찍고 다시 수면으로 올라가보겠습니다.
Response variable
크게 볼 때 우리가 다룰 모델은 다음과 같이 생겼다고 할 수 있습니다. 즉, 아래 그림에서 입력을 받아 출력을 하는 다이아몬드에 해당합니다:
모델들은 예측해야 하는 response variable 즉 $y$의 종류에 따라 바뀌게 되는데요
- Linear regression은 연속된 실수 값을 예측. temperature라고 하자.
- Logistic regression은 이진 값을 예측. cat or dog라고 하자.
- Softmax regression은 multi-class label을 예측. red or green or blue라고 하자.
각 모델에서 response variable은 서로 다른 값들을 가질 수 있습니다. 이들이 바로 random variables입니다. 그렇다면 각각의 random variable은 어떤 확률 분포를 갖을까요?
- temperature는 true mean $\mu\in(-\infty,\infty)$와 true variance $\sigma^2\in(-\infty,\infty)$를 갖는다.
- cat or dog는 고양이 혹은 강아지를 값으로 값는다. 공평한 동전 던지기가 언제나 $Pr(Head)=0.5$이듯이 각 결과에 대한 likelihood는 시간에 따라 변하지 않는다.
- red or green or blue는 빨강, 초록, 파랑 중 하나의 값을 갖는다. 마치 공평한 육면체 주사위가 그렇듯이 시간에 따라 likelihood는 바뀌지 않는다.
이런 가정들은 사실 너무 당연해서 좀 너무 진부하기까지 하지만 앞으로 얘기할 때 중요하게 사용되니 기억해둡시다.
Maximum entropy distributions
"Uber의 연간 수익"이라는 연속 값 random variable을 생각해보겠습니다. 마치
temperature와 같이 이 random variable 역시 true mean $\mu\in(-\infty,\infty)$와 true variance $\sigma^2\in(-\infty,\infty)$를 갖습니다. 당연하지만 두 경우에 대한 평균과 분산은 서로 다르겠죠. 다음과 같이 가상으로 10개의 값들을 관측했다고 해보겠습니다:
| uber | temperature |
|---|
| -100 | -50 |
| -80 | 5 |
| -20 | 56 |
| 5 | 65 |
| 15 | 62 |
| -10 | 63 |
| 22 | 60 |
| 12 | 78 |
| 70 | 100 |
| 100 | -43 |
이를 그려보면 다음과 같습니다:
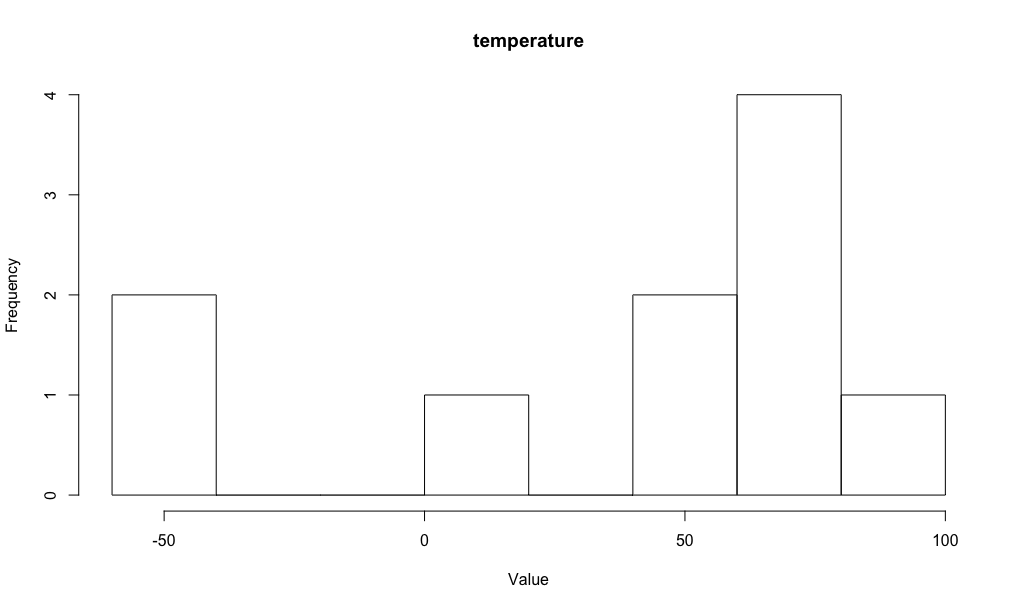
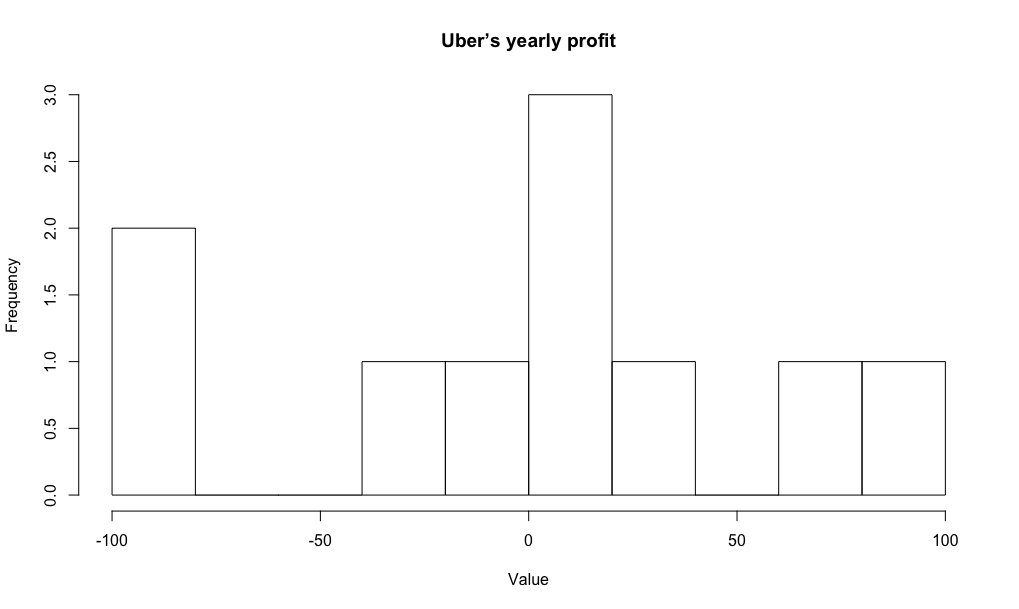
우리는 각 random variable에 대해 실제 확률 분포가 어찌 생겼는지는 모릅니다. 전반적 "형태"도 모르고 그 형태를 제어하는 parameters도 모릅니다. 이럴 때는 어떻게 모델을 정해야할까요? 사실 통계학의 정수가 바로 여기에(미지의 값들을 추측하는 것) 있습니다.
자, 초기 모델을 정하기 위해 다음의 두 가지를 염두에 두어야합니다:
- 최대한 보수적이어야 합니다. 우리는 "Uber의 연간 수익"에 대해 고작 10개의 값만을 보았을 뿐입니다. 아직 관측되지 않았다고 해서 다음 스무 개의 값들이 $[-60,-50]$ 사이의 범위에서 나올 수도 있다는 사실을 간과하고 싶지는 않겠죠.
- 각각에 대하여 동일한 가정(continuous)을 했기 때문에 두 random variables 모두에 대하여 같은 확률 분포 "모양"을 가정해야합니다.
이에 따라 매우 진부하지만 위에서 정의한 제약 조건들을 만족하는 가장 보수적인 분포를 사용하겠습니다. 이 것이 바로
maximum entropy distribution입니다.
* (편집자 주) 그냥 이렇게 넘어가면 사실 왜 maximum entropy distribution을 사용해야하는지 잘 와닿지 않을 수 있으니 제가 첨언을 좀 해보겠습니다.
통계나 정보 이론에서 maximum entropy probability distribution은 이름이 의미하듯 분포가 갖는 엔트로피 값이 해당 class의 확률 분포들이 가질 수 있는 최대 엔트로피 값과 최소한 같거나 큽니다.
무슨 말인고 하니, 만약 우리가 어떤 모델을 세울 때 해당 데이터에 대해 알고 있는 정보가 적다면 잘못된 선험적 정보를 부지불식간에 모델에 넣지 않도록 주의를 기울여야 한다는 것입니다. (maximum entropy의 원리에 따라) 모델을 정할 때 해당 데이터가 어떤 class에 속한다는 정보 외에 분포에 대한 어떠한 정보도 없을 때는 가장 기본적으로 최소한의 정보만을 사용하여(largest entropy) 분포를 정해야할 것입니다.
바로 여기에 해당하는 분포가 maximum entropy distribution인 것이죠. 이 외에도 많은 physical systems이 시간이 지나면서 점차 maximal entropy configuration을 향하기 때문에서라도 maximum entropy distribution으로 초기 모델을 정하는 것이 여러 모로 장점이 있습니다.
temperature(continuous-valued distribution)에 대한 maximum entropy distribution은 Gaussian 분포입니다. 가우시안 분포의 확률 밀도 함수는 다음과 같죠:
$$P(y\vert \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\bigg(-\frac{(y - \mu)^2}{2\sigma^2}\bigg)}$$
cat or dog에 대한 maximum entropy distribution은 binomial 분포입니다. 이항 분포의 확률 밀도 함수는 (for a single observation) 다음과 같습니다:
$$P(\text{outcome}) =
$\begin{cases}
1 - \phi & \text{outcome = cat}\\
\phi & \text{outcome = dog}\\
\end{cases}$$ (여기서 positive event에 대한 확률을 $\phi$로 표기하였습니다.)
마지막으로
red or green or blue에 대한 maximum entropy distribution은 multinomial distribution입니다. 다항 분포의 확률 밀도 함수는 다음과 같습니다:
$$P(\text{outcome}) =
\begin{cases}
\phi_{\text{red}} & \text{outcome = red}\\
\phi_{\text{green}} & \text{outcome = green}\\
1 - \phi_{\text{red}} - \phi_{\text{green}} & \text{outcome = blue}\\
\end{cases}$$
이렇게 각 모델에 대한 "maximun entropy distribution"가 위와 같이 유도된다는 것을 은근슬쩍 구렁이 담넘어 가듯이 지나갔지만 사실 이 부분은 Lagrange multipliers로 매우 명료하게 설명하는 것이 가능합니다. 이 부분은 해당 글의 범위를 넘어서거니와 이 글의 목적을 명확히 하는데 오히려 방해가 될 소지가 있기에 글쓴이가 의도적으로 내용을 생략하였습니다.
* (편집자 주) 실제로도 매우 쉽습니다. 다음에 기회가 되면 포스팅을 하도록 하겠습니다. 예를 들어 가우시안 분포는 전체 실수 선 $x\in(-\infty, \infty)$를 모두 포괄하되 유한한 평균과 분산을 갖는 모든 확률 분포에 대한 maximum entropy distribution입니다. 이렇게 maximum entropy distribution을 유도하다보면 가우시안 분포의 적분식이 왜 그렇게 생겼는지 알 수 있습니다. 재밌겠죠!
마지막으로 "Uber의 연간 수입"과
temperature 값들의 실제 분포가 가우시안으로 표현될 수 있다는 가정을 사용하긴 하였으나 사실 각각에 대해 약간씩 다른 가우시안입니다. 이는 각 random variable이 서로 다른 true mean과 variance를 갖기 때문입니다. 이 값들은 각 가우시안 분포들이 더 키가 크거나 옆으로 퍼지거나 혹은 좌우로 shift되는 정도를 다르게 조정하게 됩니다.
Functional form
이 글에서 다루고 있는 세 모델들은 각각 서로 다른 함수를 바탕으로 예측을 하는데요: 각각 identity function (i.e. no-op), sigmoid function, and softmax function. Keras로 output layer를 만들어보면 명확합니다:
output = Dense(1)(input)
output = Dense(1, activation='sigmoid')(input)
output = Dense(3, activation='softmax')(input)
이 단락에서는,
- Gaussian, binomial 그리고 multinomial distributions가 같은 functional form으로 나타낼 수 있다는 것을 보이겠습니다.
- 이 common functional form에서 세 모델들의 output function (identity, sigmoid, softmax)가 자연스럽게 유도된다는 것을 보이겠습니다.
마치 다음 그림과 같이 생각할 수 있겠네요. 세 가지 분포가 들어가서 세 가지 output functions이 나오는 것이죠. (그림이 이상한데? -_-; 뭐 아무튼 하나의 functional form으로 설명이 가능해서 저렇게 표현할 수 있다고 생각하면 될 듯합니다.)
여기서 병목에 해당하는 개념은 확률 분포의
"exponential family"가 되겠습니다.
자! 이 부분이 사실 매우매우 재미있는 부분이지만 아쉽게도 글이 매우 길어지기도 했고 글을 하루에 쓸 수 있는 양이 있으니(..orz) 다음 글에서 이어가도록 하겠습니다. (드라마도 아니고....준비 운동하다 시간이 다 갔네요..ㅋㅋ 얼른 돌아오겠습니다. )
그러면! 다음 글에서 뵙겠습니다. (To be continued)