Anyone can Learn To Code an LSTM-RNN in Python¶
[Refercence]If you want more detailed background with explanations about RNN:
원문 링크 (Eng): https://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/
번역 링크 (Kor): https://jaejunyoo.blogspot.com/2017/06/anyone-can-learn-to-code-LSTM-RNN-Python.html
깃헙 레포 (Kor, Eng): https://github.com/jaejun-yoo/RNN-implementation-using-Numpy-binary-digit-addition
[목표]¶
- 간단한 toy code로 RNN을 이해한다.
- RNN을 사용하여 이진수 더하기 연산을 학습시킨다.
[objective]¶
- Understand RNN with a simple numpy implementation.
- Train RNN for a binary opperation, e.g. addition.
- Check if the trained RNN can be extended for the unseen data with longer digits (e.g. 8 bytes digits training -> 10 bytes digit test)
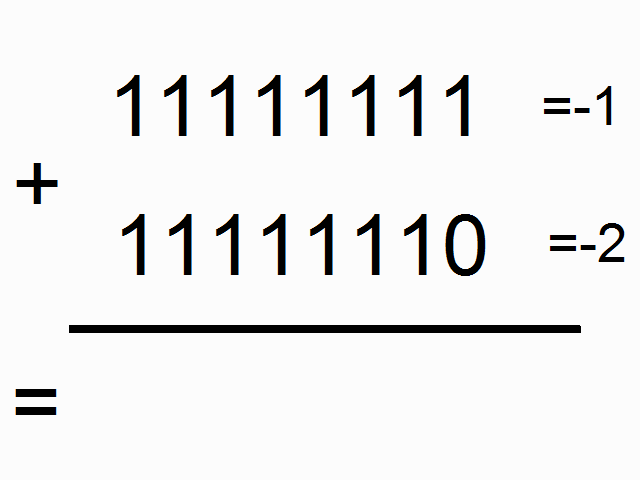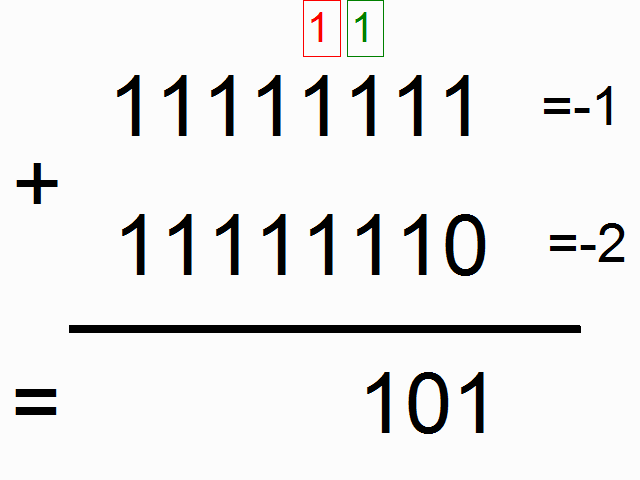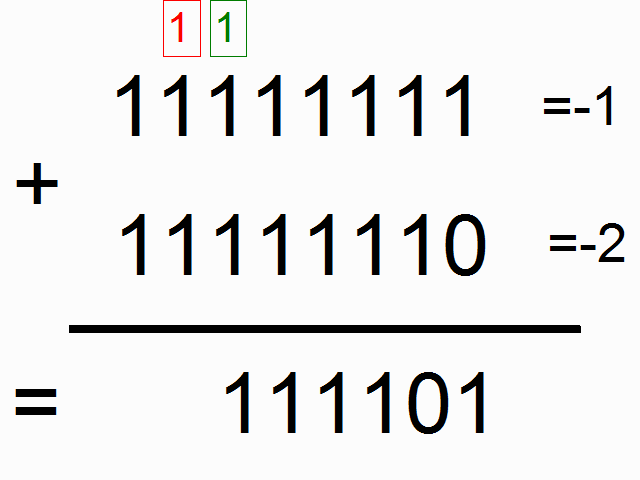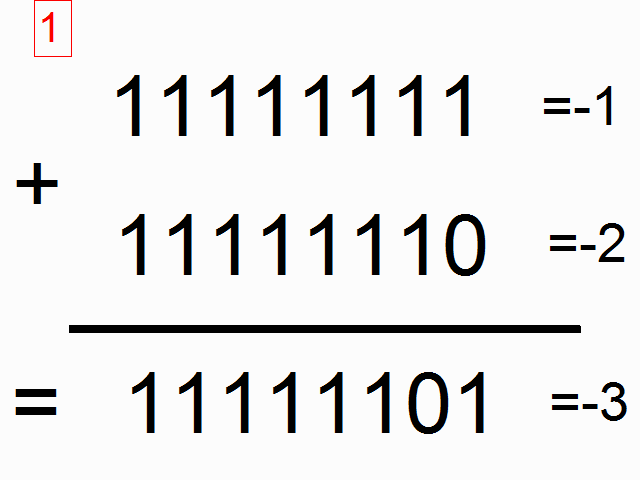
In [1]:
# Import libraries
import copy, numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
%matplotlib inline
In [2]:
# Utility functions
def sigmoid(x):
output =1/(1+np.exp(-x))
return output
def sigmoid_output_to_derivative(output):
return output*(1-output)
In [3]:
# Decide the maximum binary dimension (최대 이진수의 범위를 8 byte로 한정)
max_binary_dim = 8
largest_number = pow(2,max_binary_dim)
#print(2**8)
#print(pow(2,max_binary_dim))
#print(range(2**3))
Create binary lookup table¶
In [4]:
# Create binary lookup table (그저 편의상 만들뿐 굳이 이런 식으로 하지 않아도 됨)
# np.unpackbits e.g.
print(np.unpackbits(np.array([8], dtype = np.uint8)))
print("====================")
# 이진수로 만들 정수 값들 1~256을 list in list 형태로 만듬.
# e.g
# binary_gonna_be = np.array([range(largest_number)], dtype=np.uint8).T
# print(binary_gonna_be)
# 이런 식으로 binary lookup table 완성
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis = 1)
print(binary.shape, binary)
print("====================")
int2binary = {}
for i in range(largest_number):
int2binary[i] = binary[i]
print("lookup table test")
print(binary[3], int2binary[3])
#print(int2binary)
Initial parameter setting¶
In [5]:
alpha = 0.1 # learning rate
input_dim = 2 # 각 자리수끼리 더할 것이므로 서로 더할 두 이진수의 n번째 자리에 해당하는 digit 두 개가 input이 됨
hidden_dim = 16 # 바꾸면서 성능이 어떻게 변하는지 확인해보면서 놀아보자, You can vary this and see what happens
output_dim = 1 # output은 결국 n번째 자리의 digit 두 개가 합해서 나올 값이므로 one dim이 된다. e.g. 1(2) + 1(2) = 0(2) with overflow 1
# weight initialization
synapse_0 = 2*np.random.random((input_dim,hidden_dim))-1
synapse_1 = 2*np.random.random((hidden_dim,output_dim))-1
synapse_h = 2*np.random.random((hidden_dim,hidden_dim))-1
print(synapse_0.shape, synapse_1.shape, synapse_h.shape)
In [6]:
# saving for updates and visualization
s0_update = np.zeros(synapse_0.shape) # s0_update = np.zeros_like(synapse_0)
s1_update = np.zeros(synapse_1.shape)
sh_update = np.zeros(synapse_h.shape)
overallError_history = list()
accuracy = list()
accuracy_history = list()
accuracy_count = 0
training!!¶
In [7]:
max_iter = 20000
for j in range(max_iter):
# 랜덤하게 정수 두 개를 뽑은 후 binary lookup table에서 해당 이진수 가져오기.
# Randomly pick two integers and change it to the binary representation
a_int = np.random.randint(1,largest_number//2)
a = int2binary[a_int]
b_int = np.random.randint(1,largest_number//2)
b = int2binary[b_int]
# 실제 정답 계산 및 binary 벡터 저장.
# Calculate the answer and save it as a binary form
c_int = a_int + b_int
c = int2binary[c_int]
# RNN이 예측한 binary 합의 값 저장할 변수 선언.
# Declare the variable for saving the prediction by RNN
pred = np.zeros_like(c)
overallError = 0
output_layer_deltas = list()
hidden_layer_values = list()
hidden_layer_values.append(np.zeros(hidden_dim)) # dim: (1, 16)
# feed forward !
# 이진수의 가장 낮은 자리수부터 시작해야하므로 reversed로 for문 돌림.
# As you have to calculate from the "first" position of the binary number, which stands for the lowest value, loop backward.
# e.g.
# 10(2) + 11(2), for the first iteration: X = [[0,1]] y = [[1]]
for position in reversed(range(max_binary_dim)):
# RNN에 들어갈 input과 output label 이진수 값 가져오기
# Take the input and output label binary values
X = np.array([[a[position],b[position]]]) # dim: (1, 2), e.g. [[1,0]]
y = np.array([[c[position]]]) # dim: (1, 1), e.g. [[1]]
# hidden layer 계산하기 h_t = sigmoid(X*W_{hx} + h_{t-1}*W_{hh})
hidden_layer = sigmoid(np.dot(X,synapse_0) + np.dot(hidden_layer_values[-1],synapse_h)) # dim: (1, 16)
# output_layer 계산하기
output_layer = sigmoid(np.dot(hidden_layer,synapse_1)) # dim: (1, 1), e.g. [[0.47174173]]
# error 계산
output_layer_error = y-output_layer # dim: (1, 1)
# display를 위한 저장 (just for displying error curve)
overallError += np.abs(output_layer_error[0]) # dim: (1, )
# 이 후 backpropagation에서 사용될 delta 값 미리 계산하여 저장
# Save it for the later use in backpropagation step
output_layer_deltas.append((output_layer_error) * sigmoid_output_to_derivative(output_layer))
# 현재 자리수에 대한 예측값 저장
# save the prediction by my model on this position
pred[position] = np.round(output_layer[0][0])
# 현재까지 계산된 hidden layer 저장
# save the hidden layer by appending the values to the list
hidden_layer_values.append(copy.deepcopy(hidden_layer))
if (j%100 == 0):
overallError_history.append(overallError[0])
# 이제 backpropagation !
# 맨 처음 시작할 때는 현재 시점보다 앞에 있는 hidden layer가 없으므로 delta 값이 0임.
# As RNN needs to consider the "future" hidden layer value to calculate the backpropagation and it does not have the
# value at the first time (at the end of the position where backpropagation starts), we have to initialize it with zeros
future_hidden_layer_delta = np.zeros(hidden_dim)
# backpropagation을 할 때는 이진수의 가장 앞자리수 시점부터 돌아와야 하므로 정상적인 for문
# Now it should go "backward" which means an ordinary way in the for loop
for position in range(max_binary_dim):
# 필요한 값들 다시 불러오고
# bring what you needs for calculation
X = np.array([[a[position],b[position]]])
hidden_layer = hidden_layer_values[-position-1]
prev_hidden_layer = hidden_layer_values[-position-2]
# 현재 시점에서 output layer error로부터 돌아오는 gradient 값
# Get the gradients flowing back from the error of my output at this position, or time step
output_layer_delta = output_layer_deltas[-position-1]
# 현재 시점의 hidden layer에 더해진 gradient를 계산하기 위해서는
# 이전 시점의 hidden layer로부터 돌아오는 error gradient + 현재 시점 output layer로부터 돌아오는 error gradient
# 이 둘의 합에 sigmoid의 derivative 계산해줘야 함
# 이유: h_t = sigmoid(X*W_{hx} + h_{t-1}*W_{hh})를 역전파 하는 것을 생각하면 됨.
# Important part! (Backpropagation)
# Think about the feed forward step you have done before: h_t = sigmoid(X*W_{hx} + h_{t-1}*W_{hh})
hidden_layer_delta = (np.dot(future_hidden_layer_delta,synapse_h.T) + np.dot(output_layer_delta,synapse_1.T)) \
* sigmoid_output_to_derivative(hidden_layer)
# 8자리 모두를 다 계산한 후 gradient의 합을 한 번에 update 해준다.
# 이유: backprop이 아직 다 끝나지 않았는데 중간에 hidden layer의 value가 바뀌면 안됨
# Save the updates until the for loop finishes calculation for every position
# Hidden layer values must be changed ONLY AFTER backpropagation is fully done at every position.
s1_update += np.atleast_2d(hidden_layer).T.dot(output_layer_delta)
sh_update += np.atleast_2d(prev_hidden_layer).T.dot(hidden_layer_delta)
s0_update += X.T.dot(hidden_layer_delta)
# 다음 position으로 넘어가면 현재 hidden_layer_delta가 future step이 되므로 이를 넣어준다.
# Preparation for the next step. Now the current hidden_layer_delta becomes the future hidden_layer_delta.
future_hidden_layer_delta = hidden_layer_delta
# weight 값들 update (learning rate를 곱하여)
synapse_1 += s1_update*alpha
synapse_0 += s0_update*alpha
synapse_h += sh_update*alpha
# update value initialization for the new training data (새로운 a,b training 이진수에 대해 계산을 해줘야하므로)
s1_update *= 0
s0_update *= 0
sh_update *= 0
# accuracy 계산
check = np.equal(pred,c)
if np.sum(check) == max_binary_dim:
accuracy_count += 1
if (j%100 == 0):
accuracy_history.append(accuracy_count)
accuracy_count = 0
if (j % 100 == 0):
print ("Error:" + str(overallError))
print ("Pred:" + str(pred)) # 예측값
print ("True:" + str(c)) # 실제값
final_check = np.equal(pred,c)
print (np.sum(final_check) == max_binary_dim)
out = 0
for index, x in enumerate(reversed(pred)):
out += x * pow(2, index)
print (str(a_int) + " + " + str(b_int) + " = " + str(out))
print ("------------")
In [8]:
#print(overallError_history)
x_range = range(max_iter//100)
plt.plot(x_range,overallError_history,'r-')
plt.ylabel('overallError')
plt.show()
plt.plot(x_range,accuracy_history,'b-')
plt.ylabel('accuracy')
plt.show()
In [9]:
# Test for the codes (garbage)
# ====================================================== #
#int('{0:09b}'.format(6))
#list(format(6, "08b"))
#results = list(map(int, list(format(6, "08b"))))
#results
#str(10)+"b"
# ====================================================== #
# create a binary digit over 8 bytes
max_binary_dim = 10
largest_number = pow(2,max_binary_dim)
digit_key = "0"+str(max_binary_dim)+"b"
np.array(list(map(int,list(format(6, digit_key)))))
Out[9]:
In [10]:
# initialization
overallError_history = list()
accuracy = list()
accuracy_history = list()
accuracy_count = 0
Everything is exactly the same except the digit length tested¶
- This time, we only need to calculate the feed-forward step to see the prediction.
In [11]:
max_iter = 10000
for j in range(max_iter):
# 랜덤하게 정수 두 개를 뽑은 후 binary lookup table에서 해당 이진수 가져오기.
a_int = np.random.randint(1,largest_number//2)
a = np.array(list(map(int, list(format(a_int, digit_key)))))
b_int = np.random.randint(1,largest_number//2)
b = np.array(list(map(int, list(format(b_int, digit_key)))))
# 실제 정답 계산 및 binary 벡터 저장.
c_int = a_int + b_int
c = np.array(list(map(int, list(format(c_int, digit_key)))))
# RNN이 예측한 binary 합의 값 저장할 변수 선언.
pred = np.zeros_like(c)
overallError = 0
output_layer_deltas = list()
hidden_layer_values = list()
hidden_layer_values.append(np.zeros(hidden_dim)) # dim: (1, 16)
# feed forward !
# 이진수의 가장 낮은 자리수부터 시작해야하므로 reversed로 for문 돌림.
for position in reversed(range(max_binary_dim)):
# RNN에 들어갈 input과 output label 이진수 값 가져오기
X = np.array([[a[position],b[position]]]) # dim: (1, 2), e.g. [[1,0]]
y = np.array([[c[position]]]) # dim: (1, 1), e.g. [[1]]
# hidden layer 계산하기 h_t = sigmoid(X*W_{hx} + h_{t-1}*W_{hh})
hidden_layer = sigmoid(np.dot(X,synapse_0) + np.dot(hidden_layer_values[-1],synapse_h)) # dim: (1, 16)
# output_layer 계산하기
output_layer = sigmoid(np.dot(hidden_layer,synapse_1)) # dim: (1, 1), e.g. [[0.47174173]]
# error 값 계산
output_layer_error = y-output_layer # dim: (1, 1)
# display를 위한 저장
overallError += np.abs(output_layer_error[0]) # dim: (1, )
# 이 후 backpropagation에서 사용될 delta 값 미리 계산하여 저장
output_layer_deltas.append((output_layer_error) * sigmoid_output_to_derivative(output_layer))
# 현재 자리수에 대한 예측값 저장
pred[position] = np.round(output_layer[0][0])
# 현재까지 계산된 hidden layer 저장
hidden_layer_values.append(copy.deepcopy(hidden_layer))
if (j%100 == 0):
overallError_history.append(overallError[0])
# accuracy 계산
check = np.equal(pred,c)
if np.sum(check) == max_binary_dim:
accuracy_count += 1
if (j%100 == 0):
accuracy_history.append(accuracy_count)
accuracy_count = 0
if (j % 100 == 0):
print ("Error:" + str(overallError))
print ("Pred:" + str(pred)) # 예측값
print ("True:" + str(c)) # 실제값
final_check = np.equal(pred,c)
print (np.sum(final_check) == max_binary_dim)
out = 0
for index, x in enumerate(reversed(pred)):
out += x * pow(2, index)
print (str(a_int) + " + " + str(b_int) + " = " + str(out))
print ("------------")
error와 accuracy가 유지되는 것을 확인¶
- Check if the error and accuracy are maintained low and high
In [12]:
#print(overallError_history)
x_range = range(max_iter//100)
plt.plot(x_range,overallError_history,'r-')
plt.ylabel('overallError')
plt.show()
plt.plot(x_range,accuracy_history,'b-')
plt.ylabel('accuracy')
plt.show()
댓글 없음:
댓글 쓰기