구글이 미쳤어요
Hot한 논문은 빨리 리뷰해야 제맛이죠. 3월 31일날 arXiv에 올라온 따끈따끈한 논문인데 커뮤니티 사이트에 올라오는 글 덕에 편하게 살펴보다가 깜짝 놀랐습니다. 구글은 역시 구글인가 봅니다. 결과가 아주 어마무시하네요. 본문 중에
" We focus on the image generation task, setting a new milestone in visual quality, even at higher resolutions."라는 말이 나오는데 과연 milestone이라 자신할만한 결과입니다...이름도 정말 멋지게 잘 지었습니다. BEGAN이라니.
BEGAN으로 생성된 이미지들 (구글이 정말 미쳤습니다..)
정말 이 정도면 data augmentation을 해도 되지 않나 하는 생각이 듭니다. 이 결과만 해도 128 X 128 이미지 사이즈로 생성된 것인데 사실 확대해서 보아도 어색함을 느끼기가 어려울 정도입니다. 처음엔 실제 데이터 이미지를 소개하는 것을 잘못 이해했나 하고 캡션을 다시 봤을 정도입니다.
BEGAN의 contribution
저자들이 얘기하는 BEGAN의 contribution은 다음과 같습니다 (하나하나 따로만 봐도 빠질 것이 없네요):
- 단순하지만 강력한 구조와 빠르고 안정적인 학습과 수렴이 가능한 GAN
- Discriminator와 generator 사이의 균형을 조정해주는 equilibrium contept
- 이미지의 다양성과 질(quality) 사이의 trade-off를 조정하는 것이 가능한 새로운 방법
- "수렴"의 approximate measure
BEGAN은 기본적으로 앞서 나온 EBGAN과 WGAN에서 얻은 아이디어와 지금까지 개발된 다른 테크닉을 잘 사용해서 (물론 새로운 아이디어도 많이 있으나) 이렇게 좋은 결과를 만들어냅니다. 여기에 더해 (이미 알려진 것을 잘 사용하는 것도 정말 능력입니다만 이렇게까지 좋게 만들 수 있을 지는 상상도 못했네요.)
일단 BEGAN은 EBGAN과 상당히 닮은 뼈대를 가지고 있습니다. EBGAN이 discriminator에 auto-encoder를 사용하였던 것과 마찬가지로 BEGAN도 auto-encoder를 사용합니다. 다만 한 가지 중요한 다른 점은 일반적인 GAN이 data distribution을 맞추기 위해 학습하는 것에 반해 BEGAN은 auto-encoder loss distribution을 맞추려 한다는 것입니다. 이 때 Wasserstein distance를 사용한다는 점도 per-pixel Euclidean distance를 사용하는 EBGAN과는 다른 점입니다.
Wasserstein distance for auto-encoders
위에서 얘기했듯이 BEGAN은 data distribution이 아닌 loss distribution에 더 집중합니다. 이로 인해서 어떤 다른 점이 생기는지 살펴보겠습니다.
먼저 살펴볼 부분은 loss의 분포에 관한 내용입니다. Pixel-wise loss 혹은 error들이 서로 independent하고 identically distributed라고 할 때, 우리가 잘 아는 (혹은 익숙한..ㅋㅋ) Central Limit Theorem에 의해 image-wise loss는 정규분포를 따른다고 근사할 수 있습니다. 위에서 언급한 내용들을 수식으로 정리해보겠습니다:
$\cal{L}:\mathbb{R}^{N_x}\mapsto \mathbb{R}^+$가 pixel-wise auto-encoder loss라 할 때,

BEGAN에서는 $\eta=1$로 $L_1$ norm을 사용하여 이미지와 auto-encoder로 복원된 이미지 사이의 loss를 계산하였습니다.
두 정규분포 $\mu_1=N(m_1,C_z)$와 $\mu_2=N(m_2,C_z)$에서 각각의 평균과 분산이 $m_{1,2}\in\mathbb{R}^p$, $C_{1,2}\in\mathbb{R}^{p\times p}$일 때, squared Wasserstein distance는 다음과 같습니다:
$$ W(\mu_1, \mu_2)^2=||m_1-m_2||^2_2 + trace(C_1+C_2-2(C_2^{1/2}C_1C_2^{1/2})^{1/2}$$
여기서 $p=1$을 사용하면,
먼저 살펴볼 부분은 loss의 분포에 관한 내용입니다. Pixel-wise loss 혹은 error들이 서로 independent하고 identically distributed라고 할 때, 우리가 잘 아는 (혹은 익숙한..ㅋㅋ) Central Limit Theorem에 의해 image-wise loss는 정규분포를 따른다고 근사할 수 있습니다. 위에서 언급한 내용들을 수식으로 정리해보겠습니다:
$\cal{L}:\mathbb{R}^{N_x}\mapsto \mathbb{R}^+$가 pixel-wise auto-encoder loss라 할 때,

BEGAN에서는 $\eta=1$로 $L_1$ norm을 사용하여 이미지와 auto-encoder로 복원된 이미지 사이의 loss를 계산하였습니다.
두 정규분포 $\mu_1=N(m_1,C_z)$와 $\mu_2=N(m_2,C_z)$에서 각각의 평균과 분산이 $m_{1,2}\in\mathbb{R}^p$, $C_{1,2}\in\mathbb{R}^{p\times p}$일 때, squared Wasserstein distance는 다음과 같습니다:
$$ W(\mu_1, \mu_2)^2=||m_1-m_2||^2_2 + trace(C_1+C_2-2(C_2^{1/2}C_1C_2^{1/2})^{1/2}$$
여기서 $p=1$을 사용하면,
$$ W(\mu_1, \mu_2)^2=||m_1-m_2||^2_2 + trace(c_1+c_2-2\sqrt{c_1c_2})$$
위와 같이 단순하게 바뀌고,
위와 같이 단순하게 바뀌고,
$\frac{(c_1+c_2-2\sqrt{c_1c_2})}{||m_1-m_2||^2_2}$ is constant or monotonically increasing w.r.t $W$
$$W(\mu_1, \mu_2)^2\propto ||m_1-m_2||^2_2 ~~~~~~~(*)$$
로 문제를 단순하게 만들 수 있습니다. 즉, 실험적으로 $||m_1-m_2||^2_2$만 optimize해도 $W^2$를 optimize하는데 충분합니다.
이 때, 진짜 이미지의 image-wise loss 정규분포와 가짜 이미지의 image-wise loss 정규분포 사이의 Wasserstein distance를 계산하겠다는 것이 아이디어의 핵심입니다.
약간 이상하죠? 지금까지 본 GAN들은 모델의 분포와 진짜 데이터의 분포 사이의 거리를 계산하였다면 여기서는 각각에 대해 auto-encoder error들을 계산하여 이 두 error 분포의 거리를 계산합니다.
* 짚고 넘어가기
그런데 위에서 얘기한 조건이 쉽게 성립하는가? 라는 의문이 드실 수 있습니다 (질문을 해주신 Ken Geonmin Kim님 감사합니다). 뒤에 다시 살펴보고 저도 놀랐는데 논문에 이 후 언급이 없더군요?! 아주 제한된 조건인 것이 맞고 확률분포가 가령 stationary process에서 sampling 되거나 ergodic이라면 저 조건을 만족합니다.Stationary process라 함은 1. 평균이 지점별로 모두 같고 2. 공분산이 각 지점별 거리에만 depend하다는 조건이 들어가는데 pixel space가 이를 만족할 이유가 없죠. Ergodic은 주기함수 같은 녀석이라 생각하시면 됩니다. 시간에 따라 크게 변하지 않고 어느 정도 평균처럼 움직이는 녀석입니다.
저자들이 좀 더 성실했다면 어떤 확률 분포가 저 가정을 만족하는지 실험을 해주었을텐데 뭐...결과가 잘 나오니 할 말은 없습니다ㅋㅋ(결과가 깡패죠...orz)
GAN objective
$\mu_1$을 진짜 데이터의 loss에 대한 정규분포 $\cal{L}(x)$, $\mu_2$를 가짜 생성 이미지의 loss에 대한 정규분포 $\cal{L}(G(z))$라고 생각해보겠습니다. 여기서 generator 함수 $G:\mathbb{R}^{N_z}\mapsto \mathbb{R}^{N_x}$이고 $z\in[-1,1]^{N_z}$는 $N_z$ dimension의 random samples에서 uniform distribution 입니다.
$m_1,m_2\in \mathbb{R}^+$ 이므로 앞에서 단순하게 바뀐 (*) 수식을 최대화하는 경우는 딱 두 가지로 갈립니다:
BEGAN은 (b)번을 택했는데 m1을 0으로 최소화하는 것이 진짜 이미지의 auto-encoder loss를 줄이는 것과 자연스럽게 맞기 때문에 그리 했다고 하네요.
GAN objective와 같이 generator와 discriminator의 loss들로 식을 나타내면 다음과 같습니다:
위 수식은 WGAN과 상당히 유사합니다만 두 가지 다른 점이 있는데요:
- 정규분포를 따르는 (따른다고 가정된) loss들 간의 분포를 맞춘다는 점,
- Wasserstein distance를 사용하는 함수를 단순화했기 때문에 더이상 k-Lipschitz 함수일 필요가 없다는 점.
허허..신기합니다. 그러면 더이상 clipping과 같은 technique을 사용하지 않아도 되고 결국 hyper-parameter 하나를 없앤 것이나 마찬가지군요. 확실히 앞서 저자들이 장점이라 주장한 바와 같이 이론적이고 복잡한 내용이 걷어지고 모델이 단순하게 바뀌겠습니다. 이제 안정적으로 "잘" 되는 것을 보여주기만 하면 되겠군요.
가만히 앉아 생각을 해보시면 위의 수식이 말이 됩니다. 첫번째 $\theta_D$에 대한 식에서 generator가 만들어낸 sample에 대한 loss인 $\cal{L}(G(z_D;\theta_G);\theta_D)$는 원래 sample 이미지와 auto-encoder로 복원된 sample 이미지 사이의 loss입니다. Discriminator 입장에서는 이 녀석들이 잘 못해서 loss가 클수록 좋고 이 것이 앞에 붙어있는 - 로 나타나있습니다. 반면에 진짜 sample $x$에 대한 loss인 $\cal{L}(x;\theta_D)$는 작으면 좋겠죠 이 부분은 EBGAN과 일치합니다.
앞에 내용을 이해하셨다면 두번째 $\theta_G$에 대한 식은 자연히 따라옵니다. Generator 입장에서는 이렇게 학습된 discriminator 즉 auto-encoder가 자기가 만든 가짜 sample도 잘 복원하게 하고 싶은 것이죠.
왜 auto-encoder로 복원이 잘 되게 하는 것이 generator가 사실적인 데이터를 만드는데 도움이 되는가?라는 의문이 드실 수 있는데요. 사실 이 부분은 EBGAN을 이해하면 별 다른 설명이 필요하지 않습니다. 가볍게 직관적인 설명만 해보자면, 가짜 sample을 생성할 수 있는 generator는 변할 수 있는 반면 진짜 데이터 sample $x$는 변하지 않습니다. 즉, auto-encoder가 $x$에 대해 특징을 잘 학습하면 자연히 그 정보가 generator에 흘러들어가서 변할 수 없는 $x$가 아닌 학습이 가능한 generator가 $x$의 특징들과 맞도록 바뀐다는 것이죠. 약간 transfer learning과 같은 느낌이 아닌가 싶습니다.
Equilibrium
그런데 잘 아시겠지만 GAN에서는 generator와 discriminator 사이의 파워 게임에서 균형을 맞춰주는 것이 매우 중요합니다. 이 부분이 사실 상당히 어렵고 중요한 부분이라 parameter 수를 얼마로 정할 것이냐 즉, 모델의 크기 등을 각각 어떻게 정해서 만들어 줄 것이냐는 문제가 항상 남아있습니다. 이 균형이 잘 안 맞으면 보통 discriminator가 generator를 쉽게 이기는 경우가 많습니다.
하지만 앞서 자신들의 장점이라고 말했듯이 BEGAN에서는 이 부분도 equilibrium measure technique이라는 개념을 도입해서 일부분 해결을 해주는데요. 이 개념 덕분에 한 쪽이 좀 더 학습이 잘 된 경우에도 모델이 안정적으로 학습되게 해줍니다.
이렇게 하면서 부수적으로 $\gamma$라는 새로운 hyper-parameter가 생기는데 이 parameter도 매우 재미있습니다. 값이 변화에 따라 이미지의 질과 다양성 사이에서 조절이 가능한 knob이 생긴 느낌입니다.
한 번 빠르게 BEGAN 앞 부분을 훑어보았습니다. 첫 느낌 상으로는 논문의 결과가 워낙 좋게 나와서 Cherry picking이 아닌가 정말 저렇게 되는가 의심이 갈 정도인데 다음 편에서 이것에 대해 얘기를 좀 해볼까합니다. EBGAN도 그렇고 mode collapsing과 같은 문제가 정말 해결되면서 안정적으로 학습이 되는 것인지 (energy 함수류를 사용하면 그렇다고 주장하는데... 전 아직 잘 모르겠습니다.) 등 의문점이 좀 남아있습니다.
아무튼 equilibrium 남은 내용부터 해서 좀 더 쭉 설명할 부분이 남아있으나 이미 글이 상당히 길어졌기에 다음 편에 이어서 리뷰해보도록 하겠습니다.
다음편 예고
아무튼 equilibrium 남은 내용부터 해서 좀 더 쭉 설명할 부분이 남아있으나 이미 글이 상당히 길어졌기에 다음 편에 이어서 리뷰해보도록 하겠습니다.
다음 읽을거리
- 초짜 대학원생의 입장에서 이해하는 BEGAN: Boundary Equilibrium Generative Adversarial Networks (2)
- 초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets (1)
- 초짜 대학원생의 입장에서 이해하는 Domain-Adversarial Training of Neural Networks (DANN) (1)
- 초짜 대학원생의 입장에서 이해하는 Deep Convolutional Generative Adversarial Network (DCGAN) (1)
- 초짜 대학원생의 입장에서 이해하는 Unrolled Generative Adversarial Networks (1)
- 초짜 대학원생의 입장에서 이해하는 InfoGAN (1)
- 초짜 대학원생의 입장에서 이해하는 LSGAN (1)
참고문헌:
[1] BEGAN: Boundary Equilibrium Generative Adversarial Networks David Berthelot et al. 2017


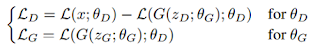
잘 보았습니다ㅎㅎ
답글삭제전개과정에서 'covar_difference/mean_difference is constant or monotonically increasing w.r.t W' 은 쉽게 성립하는 가정인가요?
감사합니다
+) 댓글이 수정은 안되네요ㅠㅠ
안녕하세요 Ken Geonmin Kim님 답변이 늦어 죄송합니다. 이 부분도 제가 간과한 부분인데 좋은 질문 감사합니다. 덕분에 다시 보게 되었네요 ㅎㅎ 당연히 쉽게 성립하는 가정이 아닙니다! 저도 놀랐는데 논문에 이 후 언급이 없더군요?!!! 다시 한 번 놓친 부분을 집어주셔서 감사합니다.
삭제아주 제한된 조건인 것이 맞고 확률분포가 가령 stationary process에서 sampling 되거나 ergodic이라면 저 조건을 만족합니다. Stationary process라 함은 1. 평균이 지점별로 모두 같고 2. 공분산이 각 지점별 거리에만 depend하다는 조건이 들어가는데 pixel space가 이를 만족할 이유가 없죠. Ergodic은 주기함수 같은 녀석이라 생각하시면 됩니다. 시간에 따라 크게 변하지 않고 어느 정도 평균처럼 움직이는 녀석입니다. 이 부분은 저도 임성빈이라는 아는 박사님께 도움을 받았네요 ㅎㅎ 다시 한 번 좋은 질문 감사합니다.
안녕하세요 BEGAN을 이해하는데 많은 도움이 되었습니다. 좋은 글 감사합니다. 그런데 아직 stationary이거나 ergodic일 경우 조건을 만족한다는 부분이 잘 이해가 되지 않는데 추가 설명해 주실 수 있나요??
삭제R의 지수부분에 N_x나 +가 올라가 있으면 어떠한 뜻인지 알려주실 수 있으신가요?
답글삭제R^3 이면 3차원 이런식으로는 이해가 가는데
N_x + 와 같은 notation은 처음보는데 수알못을 위해서 설명 부탁드립니다!..
안녕하세요 HS Choi님 댓글 감사합니다. N_x는 어떤 숫자이고 여기서는 pixel 수가 되겠네요. R^3이 3차원인 것처럼 N_x 차원을 의미합니다. +는 양수 값을 가지는 1차원을 의미하구요.
삭제쭉 보다 보니, 조금 의아한 부분이 있어서 질문드립니다!
답글삭제본 논문에서는 특정 이미지와 오토인코더를 거친 이미지 사이의 픽셀사이의 loss들이 iid할테니 그 이미지에대한 모든 pixel loss sum들은 CLT에 따라서 정규분포를 따를것이다 라고 설명하고 있는 것 같은데요, 궁금한점은 요약해주신 부분에 p=1을 선택하는 것을 pixel wise기 때문이다 라고 써주셨는데, 이게 맞는 건지 잘 모르겠습니다. CLT라는 것이 그 sum들에 대해서 성립하는 것인데, 다시 pixel wise로 돌아와 버리면 그 가정이 다 깨지는 것이 아닌가 싶습니다. 그래서 저는 저자가 p=1이라고 한 이유는 우리가 스칼라 값인 로스에 대해서 그 분포 차이를 보는것이기 때문이라고 생각했는데, 좀 더 자세한 설명 부탁드립니다!..
안녕하세요 좋은 질문 감사합니다. 아무래도 제가 간과한 부분인 것 같습니다. 먼저 해당 부분을 인용하면 다음과 같은데요 "For a sufficient large number of pixels, if we assume that the losses at the pixel level are iid distributed, then the CLT applies and the overall distribution of image-wise losses follws an approximate normal distribution." 질문해주신 부분 중 pixel loss sum이라고 하신 부분을 제가 이해한대로 부연해보자면 CLT는 동일한 확률분포를 가진 독립 확률 변수 n개의 평균의 분포가 n이 적당히 크다면 정규분포에 가까워진다는 정리이니 지금 저기서 얘기하는 것은 이미지 하나에 대해 각각의 pixel loss들의 평균을 모든 이미지 sample들에 대해 모아놓고 보면 sample 수가 많아지면 정규분포를 따른다로 이해하는 것이 맞다는 말씀이시죠? 제가 이해하기에도 그런 것 같습니다. 바로 윗 댓글에서 질문 주셨던 부분과 이어져서 loss 함수가 주는 것이 + 양수 scalar이니 p=1은 여기서 나오는 것이구요. BEGAN이 나오자마자 보고 너무 결과가 좋아 흥분해서 skim through하고 바로 정리해서 올리다보니 p가 pixel의 약자라 생각하고 넘어간 모양입니다 ㅎㅎ 좋은 질문 감사합니다 :) 혹시나 제가 잘못 생각하고 있다면 얘기해주세요 ㅎ
삭제혹시 W (b)의 경우와 L이 어떻게 연결되는지 설명해주시면 감사하겠습니다.
답글삭제m1이 0으로 간다는 것은 AE의 복원 오류가 0으로 간다는 것과 통한다는 점은 설명이 있어서 이해를 했는데 m2->inf 가 W->inf로 이어지고 W를 키우는 것이 LD나 LG를 줄이는 것과 어떻게 연결되는 지를 도통 모르겠습니다.
안녕하세요, BEGAN에 관한 질문이라기보다는 GANs에서 latent space에 관한 질문을 여쭙고자 댓글 남겨봅니다...
답글삭제GAN에서 latent space의 z vector는 보통 uniform또는 guassian 에서 sampling 하는 것 같은데 두 개의 distribution에서 sampling 하는 이유 혹은 각각이 가지는 장단 점이 있을까요?
추가로 여러가지 GAN모델에서 저마다 조금씩 다른 latent space의 크기를 산정하는 것 같은데, 예를 들어 DCGAN은 100차원 벡터를 사용하는데, 그 크기는 왜 100차원이며 그 차원의 수는 어떻게 결정하는 것인가요?...
항상 친절히 답변해주셔서 감사드립니다.
감사합니다.
오타: equilibrium contept ==> equilibrium concept
답글삭제포스팅하신 이후에 올라온 v3부터는 squared wasserstein distance 부분을 단순 wasserstein-1 distance로 변경하고, jensen inequality로 |m1 -m2| 구하는 식으로 변경되었더군요.. 위에 언급하셨던 문제 때문이었겠지요?
답글삭제BEGAN에서 fully connected를 제외한다고 하셨는데요, 그러면 신경망이 SGD같은걸로 학습이 가능한가요....? 이부분이 잘 이해가 안가서요...
답글삭제