초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (2)

* Auto-Encoding Variational Bayes, Diederik P. Kingma and Max Welling 2014를 바탕으로 한 리뷰

저번 글에 이어 Variational bound에 대한 얘기를 마치고 VAE가 기존 방식들과 어떻게 다른지, 장점은 무엇인지 등을 살펴보겠습니다.

Variational Inference

Variational inference의 기본 아이디어는 우리가 posterior inference를 어떻게 할 지 알고 있는 모델 $Q_\phi$를 가지고 inference를 하되 parameter $\phi$를 잘 조정해서 $P$에 최대한 가깝게 만들자는 것입니다.

이 때, 두 분포가 "가깝다"는 것을 어떻게 표현할 수 있을까요? 여기서 두 분포의 차이를 계산해주는 Kullback Leibler divergence가 사용됩니다:

$$KL(Q_\phi(Z|X)||P(Z|X)) = \sum_{z\in Z}q_\phi(z|x)\log\frac{q_\phi(z|x)}{p(z|x)}.$$

사실 이 녀석의 정확한 full name은 reverse KL divergence인데요 forward KL divergence와의 차이는 나중에 소개하도록 하겠습니다. 일단 여기서는 위에서 해주고자 하는 역할이 KL divergence로 실제 distribution이 $P(Z)$일 때, $Q_\phi(Z)$가 얼마나 다른지를 측정해준다고 생각하시면 됩니다. 이제 이 차이를 최대한 줄이고 싶다면 parameter $\phi$를 잘 조정해서 KL divergence가 최소화되도록 해주면 되겠습니다.

Mean-field Approximation

사실 이런 아이디어는 전통적으로 Variational Bayesian (VB) 관점으로 문제를 푸는 쪽에서 이미 많이 연구되었습니다. 앞서 소개했던 내용과 같이 Bayesian posterior inference를 할 때 계산이 불가능한 분모 $p(x)$ 부분을 해결하기 위해 variational inference 아이디어가 사용됩니다. 이를 Mean-field approximation이라 하는데요 Bayesian posterior density인 $p(\theta|x)$를 좀 더 간단한 $g(\theta|\phi)$라는 새로운 parameter $\phi$에 대한 density로 근사합니다. 이 때,

$$g(\theta|\phi)=\prod_{j=1}^J g_j(\theta_j|\phi_j)$$

와 같이 각 $\theta=\theta_1,\cdots,\theta_J$에 대해 density $g$가 factorize되는 형태를 취하고 이를 mean-field form of variational inference라고 합니다. 따라서 위에서와 마찬가지로, $$\phi^*=arg\min_\phi KL(g(\theta|\phi)||p(\theta|x))$$를 푸는 것이 VB에서 해결할 문제가 됩니다.

여기서 variational inference의 강력한 점이 하나 나오는데 바로

"본디 posterior를 estimation하는 statistical inference였던 문제를 optimization 문제로 바꿔준다는 것"이죠.

Optimization이 보통 MCMC를 이용한 posterior estimation 방식보다는 훨씬 빠르고 쓸 수 있는 도구들이 많기 때문에 이는 매우 강력한 치환입니다.

다만, 전통적인 variational inference 방식은 posterior가 언제나 근사일 뿐이라는 단점도 있고 (물론 D. Mackay가 말했듯이 아무리 나쁜 근사일지라도 최소한 point estimate인 delta function보다는 무조건 낫다고 하지만...), 위에서 가정하듯 $g$가 simple density들로 factor되는 녀석들로 나타나야한다는 것 때문에 근사를 할 수 있는 모델이 한정되는 문제가 있습니다.

게다가 likelihood와 posterior를 동시에 update하는 것이 아닌 한 쪽을 고정하고 다른 쪽을 alternative하게 계산하는 방식을 취하기 때문에 기본적으로 iteration을 하는 전략을 사용할 수 밖에 없다는 점도 한계입니다.

* 약간 미리니름하자면 DNN이 이런 optimization 문제를 일반적으로 잘 푼다는 것이 알려져있기 때문에,

1. variational inference의 아이디어를 이용해서 기존 문제를 optimization으로 바꿔주고, 
2. 이렇게 바뀐 문제를 iterative update 방식 대신 posterior $q(z|x)$와 likelihood $p(x|z)$가 각각 encoder와 decoder인 Auto-Encoder로 모델링하여 
3. 이를 NN의 강력한 도구인 gradient descent를 사용하여 한 방에 update하겠다 

는 전략으로 문제를 푼 것이 VAE입니다.

The variational bound

그래서 지금까지 소개한 얘기들을 바탕으로 실제 문제가 어떤 식으로 formulate되는지를 적어보겠습니다.

우리가 다른 모델로 바꿔 풀려고 하는 marginal likelihood $\log p_\theta(x)$를 다음과 같이 각각의 data point들에 대한 marginal likelihood들의 합으로 나타낼 수 있습니다: $$\log p_\theta(x^{(1)},\cdots,x^{(N)})=\sum_{i=1}^{N}\log p_\theta (x^{(i)}).$$ 이 때, 개별 data point들에 대한 marginal likelihood는 다음과 같습니다:

$$\log p_\theta(x^{(i)})=D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z|x^{(i)}))+\mathbb{E}_{q_\phi(z|x)}\left[-\log q_\phi (z|x) + \log p_\theta(x,z) \right].$$

RHS에서 첫번째 항을 보시면 진짜 posterior와 근사값에 대한 KL divergence이므로 항상 0보다 크거나 같은 양수임을 알 수 있고, 따라서 두번째 항이 variational lower bound가 되는 것은 자명합니다:

$$\log p_\theta(x^{(i)}) \geq \mathbb{E}_{q_\phi(z|x)}\left[-\log q_\phi (z|x) + \log p_\theta(x,z) \right]=\cal{L}(\theta,\phi;x^{(i)}).$$

위 수식은 또 다음과 같이 풀어 쓸 수 있습니다 (복잡해 보이지만 모두 정의를 집어넣고 전개하는 것 밖에 없습니다):

$$\cal{L}(\theta,\phi;x^{(i)})=-D_{KL}(q_\phi(z|x^{(i)})||p_\theta(z))+\mathbb{E}_{q_\phi(z|x^{(i)})}\left[\log p_\theta(x^{(i)}|z) \right].$$

이 식을 잘 보면 상당히 재미있는 해석이 가능해집니다. 우리의 목표는 이제 lower bound $\cal{L}$을 maximize하도록 $\theta$와 $\phi$ parameter들을 조정해주는 것으로 바뀌었고:

$$(\theta^*,\phi^*)=\arg\max_{\theta,\phi} \cal{L}(\theta,\phi;x^{(i)}),$$

앞선 식에 대해 곰곰히 생각해보면, 위 문제를 푼다는 것은:

maximum likelihood $\log p_\theta(x^{(i)}|z)$ 문제를 푸는데, 거기에 variational approximation $q_\phi(z|x^{(i)})$와 Z에 대한 prior $p_\theta(z))$ 사이의 차이가 최소가 되도록 하는 regularization 항을 추가하여 optimization 문제를 푸는 것으로 생각할 수 있습니다. 

즉, 문제를 정의하고 나니 해석이 꽤 그럴듯하게 됩니다. Maximum likelihood 문제는 결국 regression 문제로 생각하면 평균값으로 fitting해주는 문제가 되고 여기에 우리가 모델로 근사한 posterior와 prior 분포가 일치하도록 하는 제약이 추가되어 좀 더 나은 parameter를 찾고자 하는 것이죠.

보통 모델 $Q(Z|X)$ 분포가 conditionally Gaussian이라 가정하면,  prior $P(Z)$를 평균 0 분산이 1인 Gaussian 분포로 놓고 예쁘게(analytic하게) 계산하는 것이 가능합니다.

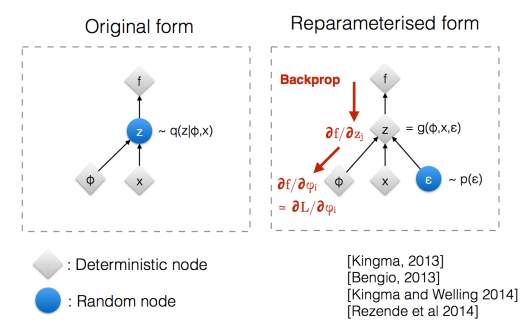
The reparameterization trick

이제 문제도 다 설정했고 , $p_\theta(\cdot)$와 $q_\phi(\cdot)$를 NN으로 모델링하여 풀기만 하면 되겠군요! 그런데 여기서 아직 해결되지 않은 부분이 있습니다. $\mathbb{E}_{q_\phi(z|x^{(i)})}\left[\log p_\theta(x^{(i)}|z) \right]$ 부분을 잘 보시면 $\mathbb{E}_{q_\phi(z|x^{(i)})}(\cdot)$으로 q로부터 sampling을 해서 계산을 하게 되어있죠. 이 때 이 문제를 NN으로 풀 경우, feed-forward 계산은 아무런 문제가 없습니다. 그냥 현재 $Q_\phi(Z|X)$ 분포에서 $z$를 여러 개 sampling해서 $P_\theta(X|Z)$에 넣어 계산하면 되니까요.

문제는 backward일 때입니다. 우리는 NN으로 모델을 정의했을 때 가지고 올 수 있는 강력한 도구인 gradient descent 혹은 ascent를 사용하고 싶은데, sampling은 미분이 가능한 연산이 아니기 때문에 back-propagation으로 문제를 풀 수가 없습니다. NN으로 정의한 모델을 gradient descent로 푼다는 것은 모델이 parameter에 대해 미분이 가능하고 이는 모델이 어떤 의미에서는 deterministic하다는 것을 의미합니다. 즉, fixed parameter들에 대해 stochasticity는 input에만 있고 같은 input에 대해서는 항상 같은 output이 나와야 하는데 이 "sampling"이란 녀석은 모델 자체에 stochasticity를 넣어버리기 때문에 문제가 됩니다. 

이걸 아주 교묘하게 우회하는 방법을 "reparameterization trick"이라 하는데요 이게 또 기가 막힙니다. 이건 다음 글에 또 이어서 얘기해보도록 하겠습니다. 

음... 확실히 VAE는 좀 이론적인? 배경을 설명할 부분이 많아서인지 그림은 없고 글로만 쭉쭉 채우네요. 다음에는 결과도 넣고 도표도 만들어 넣고 좀 더 재미있게 써봐야겠네요. 

다음 읽을거리

• 초짜 대학원생의 입장에서 이해하는 Auto-Encoding Variational Bayes (VAE) (3)
• 초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets (1)
• 초짜 대학원생의 입장에서 이해하는 Domain-Adversarial Training of Neural Networks (DANN) (1)
• 초짜 대학원생의 입장에서 이해하는 Deep Convolutional Generative Adversarial Network (DCGAN) (1)
• 초짜 대학원생의 입장에서 이해하는 Unrolled Generative Adversarial Networks (1)
• 초짜 대학원생의 입장에서 이해하는 InfoGAN (1)
• 초짜 대학원생의 입장에서 이해하는 LSGAN (1)
• 초짜 대학원생의 입장에서 이해하는 BEGAN: Boundary Equilibrium Generative Adversarial Networks (2)

참고문헌:

[1] Auto-Encoding Variational Bayes, Diederik P. Kingma and Max Welling 2014

[2] NIPS 2016 Tutorial: Generative Adversarial Networks, Ian Goodfellow 2016

[3] A Beginner's Guide to Variational Methods: Mean-Field Approximation

[4] KL Divergence: Forward vs Reverse?

[5] Variational Autoencoder: Intuition and Implementation

[6] Tutorial: What is a variational autoencoder?

[7] Slides: Introduction to variational autoencoders