초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets (1)

* Generative Adversarial Nets - Ian Goodfellow et al. 2014 논문을 기본으로 작성한 리뷰. 

NIPS 2016에서 가장 hot한 키워드를 하나 꼽으라 한다면 Generative Adversarial Network(GAN)이라고 단언할 수 있을 정도로 2014년에 Ian Goodfellow(이름 한 번 독특하네..웬만해서는 이름 쉽게 못 외우는데 한 번에 외웠네요 좋은 친구라니 ㅋㅋ)가 NIPS에서 발표한 paper에서 시작한 GAN 붐은 2016년에 더 크게 터진 것 같습니다.

과연 facebook의 Yann Lecun 교수님이 근 10-20년 간에 기계학습 나온 아이디어 중 최고라고 할만하구나(근데 너무 자주, 여러 번, 모든 곳에서 얘기하시는 듯...뭐..그만큼 중요하단 얘긴가...)란 느낌이 들 정도로 이미지 생성(image generation) 외에도 natural language processing(NLP) 등 다양한 분야에서 엄청난 성과들을 보여주고 있습니다.

당장 TensorFlow나 MatConvNet으로 GAN을 구현해서 뭔가 좀 더 새로운 것을 해내야...졸업을 시작?할 수라도 있을 것 같은 불쌍한 대전의 대학원생은 일단 GAN에 대해 또 열심히 공부를 하기 시작했고...orz... 그 일환으로 Ian Goodfellow의 NIPS 2014 paper를 나름대로 정리해 보았습니다.

이 paper에서 중요한 내용은 크게 두 가지로 나눌 수 있을 것 같습니다;

1. GAN에 대한 이론적 개념 제시(minimax problem)와 
2. GAN이 풀어야하는 problem이 global minimum에서 unique solution을 갖고 어떤 조건을 만족하면 해당 solution으로 수렴한다는 것을 증명.

각각에 대해 차근차근 처음 공부하던 입장에서 정리해보겠습니다.

[GAN에 대한 개념적 소개]

GAN은 이름만 뜯어봐도 일단 큰 줄기를 알 수 있습니다.

"Adversarial"이란 단어의 사전적 의미를 보면 대립하는, 적대하는 란 뜻을 갖습니다. 대립하려면 어찌 되었든 상대가 있어야하니 GAN은 크게 두 부분으로 나누어져 있다는 것을 먼저 직관적으로 알 수 있죠.

뭔가 Image를 만들어내는 녀석과(Generator) 이렇게 만들어진 녀석을 평가하는 녀석(Discriminator)이 있어서 서로 대립(Adversarial)하며 서로의 성능을 점차 개선해 나가자는 것이 주요 개념입니다.

Ian Goodfellow가 본문에서 예시로 든 것은 지폐위조범과 경찰인데 나름 재미있기도 하고 이해가 잘 되어 여기에 소개해보겠습니다.

지폐위조범(Generator)은 경찰을 최대한 열심히 속이려고 하고 다른 한편에서는 경찰(Discriminator)이 이렇게 위조된 지폐를 진짜와 감별하려고(Classify) 노력한다.
이런 경쟁 속에서 두 그룹 모두 속이고 구별하는 서로의 능력이 발전하게 되고 결과적으로는 진짜 지폐와 위조 지폐를 구별할 수 없을 정도(구별할 확률 $p_d=0.5$)에 이른다는 것.

아 정말 이해가 잘 돼...내가 이런 예화를 논문에 쓴다 그러면 우리 교수님은 장난치는거냐고 하실지도...-_- 교수님은 언제나 진지하시니까ㅋㅋ Ian Goodfellow는 논문을 정말 이해가 잘 되도록 쓰는 능력이 있는 듯 합니다. 다른 논문들도 다 글이 쉽고 수학도 그리 어렵지 않고 친절해..

아무튼 이런 예시를 좀 더 딱딱하게 수학적인 용어를 섞어 쓰면 다음과 같습니다. Generative model $G$는 우리가 갖고 있는 data $x$의 distribution을 알아내려고 노력합니다. 만약 $G$가 정확히 data distribution을 모사할 수 있다면 거기서 뽑은 sample은 완벽히 data와 구별할 수 없겠죠.
한편 discriminator model $D$는 현재 자기가 보고 있는 sample이 training data에서 온 것(진짜)인 지 혹은 $G$로부터 만들어진 것인 지를 구별하여 각각의 경우에 대한 확률을 estimate합니다.

* 그림은 Ian Goodfellow가 최근 arXiv에 올린 NIPS 2016 Tutorial: Generative Adversarial Networks에서 가져왔습니다. 다음 번 글에서는 이 튜토리얼을 쭉 다뤄볼까 싶기도 한데 워낙 소개하는 양이 방대해서 여유가 되면 하는 것으로..ㅎㅎㅎ

따라서 위 그림을 보면 알 수 있듯이 $D$의 입장에서는 data로부터 뽑은 sample $x$는 $D(x)=1$이 되고, $G$에 임의의 noise distribution으로부터 뽑은 input $z$ 넣고 만들어진  sample에 대해서는 $D(G(z))=0$가 되도록 노력합니다. 즉, $D$는 실수할 확률을 낮추기(mini) 위해 노력하고 반대로 $G$는 $D$가 실수할 확률을 높이기(max) 위해 노력하는데, 따라서 둘을 같이 놓고보면 "minimax two-player game or minimax problem"이라 할 수 있겠습니다.

여기서 잘 보면 알겠지만 $G$와 $D$는 사실 꼭 neural network로 만들 필요가 없습니다. 어떤 model이든 이 역할을 서로 "잘" 해줄 수만 있다면 상관이 없습니다만 neural network를 사용한 것이 여러모로 실제 적용시 여러 장점이 있기에(물론 단점도 있지만) 그리고 결과도 꽤 잘 나오기에 결국 Generative Adversarial Nets가 된 것으로 보입니다.

어떤 장단이 있고 "잘"하는 것이 어떤 의미인지는 나중에 소개하겠습니다.

[Adversarial Nets]

일단 $G$와 $D$가 둘 다 multilayer perceptrons model을 사용하면..

Generator's distribution $p_g$ over data $x$를 학습하기 위해 generator의 input으로 들어갈 noise variables $p_z(z)$에 대한 prior를 정의하고, data space로의 mapping을 $G(z;\theta_g)$라 표현할 수 있습니다. 여기서 $G$는 미분 가능한 함수로써 $\theta_g$를 parameter로 갖는 multilayer perceptron입니다.

한편, Discriminator 역시 multilayer perceptron으로 $D(x;\theta_d)$로 나타내며 output은 single scalar 값이 되겠다(확률이므로). $D(x)$는 $x$가 $p_g$가 아닌 data distribution으로부터 왔을 확률을 나타냅니다.

따라서, 이를 수식으로 정리하면 다음과 같은 value function $V(G,D)$에 대한 minimax problem을 푸는 것과 같아집니다;
$$\min_G \max_D V(D,G) = \mathbb{E}_{x\sim p_{data}~(x)}[log D(x)] + \mathbb{E}_{z\sim p_x(z)}[log(1-D(G(z)))]$$
뭐든지 간에 이런 수식이 있으면 극단적인 예시를 넣어 이해하는 것이 빠르죠. 먼저 가장 이상적인 상황에서의 $D$ 입장을 생각해 보겠습니다.
$D$는 아주 잘 구별을 하는 녀석이므로 $D$가 보는 sample $x$가 실제로 data distribution으로부터 온 녀석이라면 $D(x) =1$이므로 첫번째 term에서 $log$ 값이 사라지고 $G(z)$가 만들어낸 녀석이라면 $D(G(z))=0$이므로 두 번째 term 역시 0으로 사라지죠. 이 때가 $D$의 입장에서 $V$의 "최대값"을 얻을 수 있다는 것은 자명합니다.

반대로 $G$의 입장에서 생각해봐도 상황은 비슷합니다.

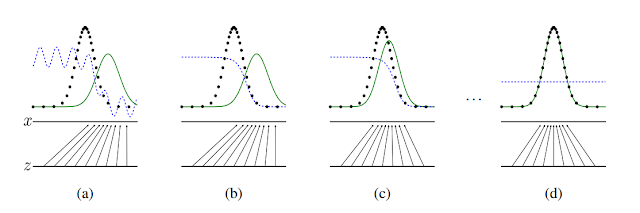
이 그림은 본 논문(NIPS 2014)에서 빌려왔습니다. 위에 설명한 내용을 아주 이해하기 좋게 잘 그려놓았는데 부연을 좀 하자면, 먼저 검은 점선이 data generating distribution, 파란 점선이 discriminator distribution, 녹색 선이 generative distribution이다. 밑에 $s$와 $z$선은 각각 $x$와 $z$의 domain을 나타내며, 위로 뻗은 화살표가 $x=G(z)$의 mapping을 보여줍니다.

즉, 처음 시작할 때는 (a)와 같이 $p_g$가 $p_{data}$와 전혀 다르게 생긴 것을 볼 수 있고 이 상태에서 discriminator가 두 distribution을 구별하기 위해 학습을 하면 (b)와 같이 좀 더 smooth하고 잘 구별하는 distribution이 만들어집니다. 이후 $G$가 현재 discriminator가 구별하기 어려운 방향으로 학습을 하면 (c)와 같이 좀 더 $p_g$가 $p_{data}$와 가까워지게 되고......
이런 식으로 쭉 학습을 반복하다 보면 결국에는 $p_g = p_{data}$가 되어 discriminator가 둘을 전혀 구별하지 못하는 즉, $D(x)=\frac{1}{2}$인 상태가 된다는 것이죠.

논문에서 한 가지 실용적인 tip이 나오는데, 위에 value function에서 $log(1-D(G(z)))$ 부분을 $G$에 대해 minimize하는 대신 $log(D(G(z)))$를 maximize하도록 $G$를 학습시킨다는 것입니다.

나중에 저자가 밝히 듯이 이 부분은 전혀 이론적인 동기로부터 수정을 한 것이 아니라 순수하게 실용적인 측면에서 적용을 하게 된 것이라 합니다.

이유도 아주 직관적인데 예를 들어 학습 초기를 생각해보면, $G$가 초기에는 아주 이상한 image들을 생성하기 때문에 $D$가 너무도 쉽게 이를 real image와 구별하게 되고 따라서 $log(1-D(G(z)))$ 값이 매우 saturate하여 gradient를 계산해보면 아주 작은 값이 나오기 때문에 학습이 엄청 느립니다.

하지만 문제를 $G = arg\max_G log(D(G(z)))$로 바꾸게 되면, 초기에 $D$가 $G$로 나온 image를 잘 구별한다고 해도 위와 같은 문제가 생기지 않기 때문에 원래 문제와 같은 fixed point를 얻게 되면서도 stronger gradient를 줄 수 있는 상당히 괜찮은 해결방법이죠.

[Theoretical Results]

앞서 말했던 두 가지 주요 내용 중 두 번째 부분입니다.
이 부분도 크게는 두 가지로 나뉘는데 먼저, 앞서 소개한 minimax problem이 $p_g = p_{data}$에서 global optimum을 갖는다는 것을 보이고 이어서 이 논문에서 소개하는 알고리즘이 global optimum을 찾는다는 것을 보이겠습니다....만,

일단 이건 다음 글에서....ㅎㅎ 이 부분도 사실 너무 쉽게 잘 설명되어 있어서 리뷰할 필요가 있나 싶네요...글이 너무 길어지는 것 같아....누가 읽기나 하려나.... 

다음 읽을거리

• 초짜 대학원생 입장에서 이해하는 Generative Adversarial Nets (2)
• [PR12-Video] 1. Generative Adversarial Nets (동영상 설명)
• GAN: 카카오 리포트 기고문 (part I) (part II)
• 초짜 대학원생의 입장에서 이해하는 Domain-Adversarial Training of Neural Networks (DANN) (1)
• Gaussian Distributions are Soap Bubbles, inFERENCe 2017. 11. 09.
• 박스 안에 넣은 공의 지름이 박스보다 클 때
• 공이 점점 비눗방울처럼 변할 때 (When ball becomes a soap bubble)

참고문헌:
[1] Generative Adversarial Nets - Ian Goodfellow et al. 2014 논문, 
[2] NIPS 2016 Tutorial: Generative Adversarial Networks