Backpropagation 설명 예제와 함께 완전히 이해하기

기계학습에 대해 관심을 갖고 신경망(Neural Networks, NN)을 처음 접하면서 가장 신비롭게 여겨졌던 부분이 바로 역전파(Backpropagation)를 통한 네트워크 학습(learning or training)이었습니다.

"신경망은 구체적으로 어떻게 학습이 되는거지?"

뭔가 직관적인 설명으로는 신경망이 계산한 답과 정답 사이의 오차를 계산하고 그 오차를 줄이도록 피드백을 주어 학습을 시킨다고 하는데....


1. 구체적으로 어떻게 그 변화 값들을 구하고 전파하는거지?

2. 그리고 그 방법이 "왜" 되는 것이지? 

그리고 역전파에 대해 어느 정도 머리로 이해하고 나서는...

생각보다 단순하고 매우 쉬운 수학만을 사용하네..
어짜피 Backpropagation은 이미 여러 라이브러리에서 잘 구현이 되어있어 사실상 내가 전혀 신경 쓸 일도 없을텐데 머리로 이해했으면 되었지 굳이 직접 손으로 풀어보고 코드를 짜보는 등 시간을 더 투자해야 할까? 등의 생각이 들었습니다.

먼저 마지막 의문에 대해서는 cs231n 수업 명강사로 유명한 Andrej Karpathy가 최근 쓴 글이 아주 잘 답변을 해주고 있죠; Yes you should understand backprop.
네 잘 알아야하고 코딩도 스스로 해봐야한다네요ㅎㅎ

저 글을 한 문장으로 요약하자면 다음과 같습니다:

"The problem with Backpropagation is that it is a leaky abstraction."

즉, 자칫하면 뉴럴 네트워크의 학습 과정을 추상적으로만 생각하고 지나가버리는 함정에 빠질 수 있다는 것!
실제로 구현해보지 않고 머리로만 이해한 사람은 신경망을 설계할 때, 단순히 layer를 쌓아주기만 하면 역전파(Backprop)가 "magically make them work on your data"라고 믿게 될 수 있으나...

실제로는 절대로 생각처럼 이상적으로 돌아가지만은 않고 여러가지 문제점들이 생길 수 있으며, 대표적으로 sigmoid나 tanh 함수가 saturate 되어 생기는 vanishing gradient 문제, dying ReLUs 문제 등을 자세히 소개해주고 있습니다. 관심있는 분들은 원글을 한 번 읽어보시길.

그럼 이 부분은 Andrej Karpathy에게 넘기고, 여기서는 첫 번째 의문에 대해 나름대로 정리해보겠습니다. 

물론 이미 같은 내용에 대한 답을 하기 위해 많은 자료들이 인터넷에 존재하고 여러 사람들이 다양한 관점으로 설명을 잘 해두었지만, 역시 무엇이든 제대로 이해하기 위해서는 스스로 시간을 투자해서 공부한 것을 나만의 언어와 논리로 정리하고 소화할 필요가 있는 것 같습니다.
이해를 위해 하는 것인데 너무 복잡한 문제로 시작하면 문제 자체보다 푸는 기술에만 집중할 수 있으니 가장 단순한 binary classification 문제에서 시작해보겠습니다. 

Classification problems with two classes (binary classification)

Binary (0 or 1) classification 문제를 풀 때, 기존의 신경망 구조는 마지막 output layer의 unit이 하나만 있어서 하나의 scalar 값을 계산하여 결과로 내보냅니다. 이 때, logistic function을 cross entropy loss function과 결합하여 사용하면 scalar 값이 0과 1 사이로 한정되면서 sum-of-squared loss와는 달리 두 가지 클래스 중 하나의 클래스에 대한 확률 값으로 자연스러운 해석이 가능해지죠.

Multiple, independent, binary classification 문제로의 확장은 아주 쉬운데, 각각의 target이 independent하므로 loglikelihood들을 더해주면 됩니다. 즉, 단일 unit이었던 때(single target)와 달리 마지막 layer에서 여러 unit을 갖습니다; 그림1. 
예시를 들자면 아마 이진 값으로 채워져있는 흑백 이미지 벡터를 생각하면 되지 않을까 싶네요. 그러면 각각의 픽셀에 대해 값이 있는지 없는지를 확률적으로 계산하는 문제가 되겠습니다. 

여기서 multi-class 문제로 좀 더 확장하는 것은 생각보다 간단하고 심지어 수식을 유도해보면 binary 문제와 거의 다를 것이 없습니다. 하지만 정작 이 글의 주제인 역전파에서 벗어날 수 있기 때문에 이 얘기는 다음에 따로 정리해보겠습니다. 

Backpropagation in 2-layer neural network

이제 이 문제를 가장 간단한 구조의 2-layer neural network로 풀기 위해 backpropagation을 계산해보며 실제로 네트워크가 어떻게 "학습"하는 지 확인해보겠습니다.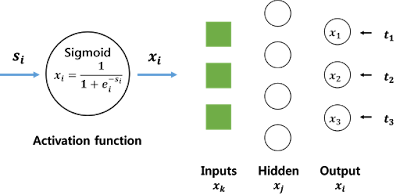

그림 1. 2-layer neural network

* Layer의 개수가 3개인데 왜 2-layer NN이라 하냐면 보통 neural network의 input layer는 세지 않기 때문에 그렇습니다.

** fully connected이기 때문에 각 층 사이에는 weight 값을 갖는 연결이 모든 조합에 대해 존재하고 편의상 그림에서는 생략해두었습니다. 

*** Hidden layer와 output layer의 activation function은 sigmoid 함수로 통일합니다. 

앞서 문제를 설정한대로 우리의 error function, E는 다음과 같습니다. 

$$E = -\sum_{i=1}^{nout}(t_i log(x_i)+(1-t_i)log(1-x_i))$$

where, $x_i = \frac{1}{1+e^{-s_i}}$, $s_i = \sum_{j=1}x_jw_{ji}$.

수식이 무엇을 의미하는지 직관적으로 이해하려면 극단적인 예제를 넣어보는게 가장 빠르죠ㅎㅎ 실제 class가 1일 때($t_i=1$), 신경망이 계산한 답이 1일 확률이 0이라는($x_i = 0$) output 결과가 나왔다고 해보고 E 값을 계산해보면 쉽게 무한대가 나오는 것을 알 수 있습니다.
반대로 제대로 확률 값이 1 즉, target $t_i$의 class가 1일 때, 실제로 1이라고 계산할 확률이 100%라고($x_i=1$) 신경망이 결과를 내었다면, E 값은 0으로 최소값을 갖습니다. 

즉, 우리의 목표는 E 값을 줄이는 것.

그럼 이제 이 오차 값을 줄이는 방향으로 네트워크를 업데이트 하면 되는데...

여기서 gradient descent라는 개념이 나옵니다. 

어떤 함수 $f$의 임의의 점 $x$에서의 구배(gradient)를 계산하면 $x$로부터 단위($\Delta x$)만큼 움직였을 때, $f$ 값이 변화하는 양을 표현하는 벡터가 나오고, 이 벡터는 항상 가장 가파르게 $f$ 값이 증가하는 방향을 가르키기 때문에 함수 $f$를 E로 두고 구배가 가르키는 반대방향(descent)으로 네트워크를 업데이트 해주면 됩니다. 

Data인 input을 바꾸는 것이 목적이 아니기 때문에 네트워크의 output 값에 영향을 주는 변수 중 우리가 수정할 것은 layer 간의 weight, $w$들입니다. 따라서 우리가 해야하는 것은 각 layer의 weight에 대한 E 함수의 gradient를 계산하고 이 변화량을 원래 w에 반대 방향 (negartive, -1)으로 더해주는 것이죠. 

신경망이 학습하는 것을 순서대로 나열해보면, Input layer로부터 각 layer를 지나치며 weight들을 곱하고, activation function을 지난 다음, 마지막 output layer에서 오차 값을 계산한 이후(feed forward), 업데이트를 위해 순차적으로 거꾸로(back) 돌아가야(propagation)합니다.
따라서 돌아갈 때 순서대로 가장 바깥 쪽 output과 hidden layer 사이의 weight부터 바꿔보겠습니다. $i$번째 output인 $x_i$에 대한 오차값에 대해 $w_{ji}$가 바뀌어야하는 정도를 계산해려면 다음과 같은 수식이 필요합니다:

$$\frac{\partial E}{\partial w_{ji}} = \frac{\partial E}{\partial x_i} \frac{\partial x_i}{\partial s_i} \frac{\partial s_i}{\partial w_{ji}}$$

1. $\frac{\partial E}{\partial x_i} = \frac{-t_i}{x_i}+\frac{1-t_i}{1-x_i} = \frac{x_i-t_i}{x_i(1-x_i)}$
2. $\frac{\partial x_i}{\partial s_i} = x_i(1-x_i)$
3. $\frac{\partial s_i}{\partial w_{ji}} = x_j$

$$\therefore \frac{\partial E}{\partial w_{ji}} = (x_i-t_i)x_j$$

(여기서 순서를 잠시 짚고 넘어갈 필요가 있습니다. 1번과 2번을 곱하면 $\frac{\partial E}{\partial s_i}$가 나옵니다. 그 후 3번을 차례로 계산하여 곱하면 결과적으로 $\frac{\partial E}{\partial w_{ji}} = (x_i-t_i)x_j$가 됩니다. 먼저 $\frac{\partial E}{\partial s_i}$를 계산했다는 것을 기억해주시면 됩니다.)

같은 논리로 그 다음 hidden과 input layer 간의 weight, $w_{kj}$에 대해 변화량을 계산하면,

$$\frac{\partial E}{\partial w_{kj}} = \frac{\partial E}{\partial s_j} \frac{\partial s_j}{\partial w_{kj}}$$

1. $\frac{\partial E}{\partial s_j} = \sum_{i=1}^{nout} \frac{\partial E}{\partial s_i}\frac{\partial s_i}{\partial x_j}\frac{\partial x_j}{\partial s_j} = \sum_{i=1}^{nout}(x_i-t_i)(w_{ji})(x_j(1-x_j))$ 
2. $\frac{\partial s_j}{\partial w_{kj}} = x_k ~(\because s_j=\sum_{k=1}x_kw_{kj})$

$$\therefore \frac{\partial E}{\partial w_{kj}} = \sum_{i=1}^{nout}(x_i-t_i)(w_{ji})(x_j(1-x_j))(x_k)$$

여기서 $x_k$는 feed forward할 때도 $i=\{1,\cdots, nout\}$까지의 모든 값에 영향을 주기 때문에 backprop 때도 $\sum_{i=1}^{nout}$을 고려하여 계산해야합니다. 위 그림에서 빨간 화살표들을 보면 되겠습니다.

여기서도 $\frac{\partial E}{\partial s_j}$를 구한 것을 보실 수 있습니다. 앞에서도 강조했었는데 이걸 기억하면 위에서 유도한 식들을 general multiplayer network로 확장하는 것도 매우 쉽습니다. 각 layer의 $\frac{\partial E}{\partial w_{ij}}$를 구하고 싶다면, 항상 $\frac{\partial E}{\partial s_j}$를 계산하고, $\frac{\partial s_j}{\partial w_{kj}} = x_k$를 곱해주는 식이 되면 됩니다. 

참고문헌: https://www.ics.uci.edu/~pjsadows/notes.pdf
(이 문헌을 참고해서 공부하긴 했지만 보시다보면 수식 전개에서 약간의 오타가 있으니 감안하고 보셔야 합니다.)